-
塑胶数 编辑
一元三次方程x^3=x+1 的实数根
塑胶数或银数是一元三次方程x^3=x+1 的唯一一个实数根,其值为约等于1.324718 。
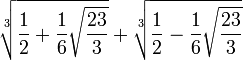 塑胶数
塑胶数
塑胶数对于佩兰数列和巴都万数列,就如黄金分割对于斐波那契数列——是两项的比的极限。它亦是最小的皮索数。
不同进制下的塑胶数数值:
二进制 | 约为1.010100110010000010110111010011101100101 |
八进制 | 约为1.246 202 672 354 510 453 326 027 421 137 040 506 046 3 |
十进制 | 约为1.324717957244746025960908854478097340734 |
十六进制 | 约为1.5320B74ECA44ADAC178897C41461334737F8172F |
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。





























